La prueba de media nula
Si queremos incorporar la variabilidad de los resultados en nuestras conclusiones, debemos comparar la dispersión de cada escenario que hemos planteado.
En general, se emplean los intervalos de confianza (IC) como medida de la dispersión, y la prueba de media nula como prueba estadística que nos permita comparar estos intervalos entre sí.
En su formulación inicial, la prueba de media nula se aplica a un resultado particular y nos permite decir si un resultado es significativamente diferente de cero para un nivel de confianza 100 X (1 - 
)%.
- Si el IC incluye el cero, no podemos decir que el resultado sea diferente de cero
- Si el IC no incluye el cero, podemos decir al 100 X (1 - 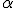)% de confianza que el resultado es diferente de cero
Ejemplo
Supón que has medido las diferencias de votos entre dos partidos políticos, A y B, en todas las circunscripciones durante los últimos 10 años. En promedio, la diferencia de votos A - B es de 2000, lo que parecería indicar que el partido A es más votado que el partido B. Sin embargo, al analizar los intervalos de confianza al 95%, obtenemos (-2000, 3000).
¿Seguirías estando seguro/a de que el partido A es el más votado?
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 3.0