Aplicación a observaciones no pareadas
La prueba de media nula también se puede aplicar aunque no tengamos las observaciones pareadas, es decir, que las dos simulaciones que estamos comparando no tengan el mismo número de observaciones o, simplemente, que no dispongamos de los resultados individuales de cada observación sino únicamente de la media y desviación estándar final de cada experimento.
Existen dos formas de aplicar la media nula en este caso.
Método 1
La más sencilla es obtener los IC de cada simulación y compararlos. Si existe solapamiento entre los IC (uno de los intervalos incluye todo o parte del otro), entonces no podemos afirmar que existan diferencias estadísticamente significativas entre las dos simulaciones. En caso contrario, podemos afirmar, al nivel de confianza que hayamos definido, que existen diferencias estadísticamente significativas entre las dos simulaciones.
Método 2
El segundo método se basa en el test de Welch, que es una formulación que emplea la distribución T de Student como referencia. Este test se emplea no solo cuando no tenemos el mismo número de observaciones, sino cuando no podemos asegurar que sus varianzas sean iguales. Deberemos calcular estimadores de la media (![]() ) y desviación estándar (Si) de cada muestra de ni observaciones. Con esos estimadores, calculamos:
) y desviación estándar (Si) de cada muestra de ni observaciones. Con esos estimadores, calculamos:
- Desviación estándar de las medias:
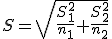
- Grados de libertad:
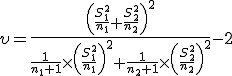
- El IC:
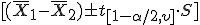
El valor de t se obtiene de las tablas de la distribución t de Student (p. ej. en Excel se haría con la fórmula "=INV.T(1-α/2; v)").
Ejemplo
Supón que contamos con los resultados agregados de dos escenarios simulados:
| Resultado | Escenario 1 | Escenario 2 |
| N | 6 | 6 |
| Media | 10,9 | 11,37 |
| Desv. est. | 2,31 | 1,33 |
Determina, con el primer método, si existen diferencias estadísticamente significativas entre los resultados de los dos escenarios.
Determina ahora, con el segundo método, si existen diferencias estadísticamente significativas entre los resultados de los dos escenarios.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 3.0