Test de Chi-Cuadrado de Pearson

Se trata de un test no parámetrico que compara los valores de la muestra con los esperados para una distribución de probabilidad continua determinada.

Para aplicarlo, se deben seguir los siguientes pasos:

1. Seleccionar el nivel de significación α
2. Construir un histograma de r intervalos con los valores observados
3. Partiendo de la estimación de parámetros de la distribución de probabilidad teórica, calcular la frecuencia esperada de valores para esta distribución en los mismos intervalos.
4. Calcular el estadístico de contraste con la fórmula 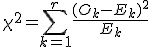, donde O_k es la frecuencia observada de valores en el intervalo k, y E_k es la frecuencia observada de valores en el mismo intervalo
5. Comparar el valor del estadístico con los valores de referencia 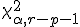, que se pueden encontrar en tablas, y donde r son los intervalos del histograma y p, los parámetros de la distribución teórica (p,.ej. para una normal p=2)

En general, cuanto mayor sea el valor del estadístico, menos verosímil es la hipótesis nula y menos probable que se trate de un buen ajuste. Por el contrario, cuanto más próximo a 0, más ajustadas estarán la distribución teórica y la de los datos observados.