Caracterización básica de variables aleatorias

Existen dos formas de visualizar la función de distribución de una v. a.

• Función de densidad de probabilidad f(x): Función que describe la probabilidad de que una variable aleatoria X asuma un cierto valor x_i.

• Función de distribución acumulada F(x): Función que describe la probabilidad de que una variable aleatoria X tenga un valor menor o igual que cierto valor x_i.

Dada una variable aleatoria, podemos hacer una primera caracterización en base a dos conceptos:

• Esperanza: Valor medio de la v.a.
• Varianza: Dispersión de la v.a. con respecto a su valor medio.

Estos dos conceptos están asociados a la población que constituye la v.a. pero, en general, únicamente disponemos de una muestra de toda la población. Supongamos que disponemos de una muestra de n elementos de la v.a. X = {x₁, x₂, ..., x_n}. En ese caso, se emplean estimadores:

Estimador de la media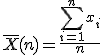
Estimador de la varianza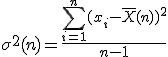

Por comodidad y por facilidad de interpretación, es más habitual calcular la raíz cuadrada del estimador de la varianza, lo que nos da la desviación típica o desviación estándar.