Técnicas para comprobar la i. i. d.
En general, la propia naturaleza de los datos puede hacer sospechar que no sean i. i. d. En esos casos en los que existe una sospecha previa, se puede representar la muestra frente al tiempo u otro factor del que creamos que depende.
Otras técnicas estadísticas son:
Gráficas de autocorrelación
Se basa en calcular la relación estadística entre cada observación y la observación a distancia (o retardo) k. Estas relaciones se representan agregadas para todas las observaciones de la muestra en una gráfica. Valores de autocorrelación cercanos a 1 o -1 indican que existe una relación estadística para esa distancia. Valores cercanos a 0 apuntan a que no existe esa relación y, por lo tanto, implicarían independencia entre las observaciones.
Más información en: https://es.wikipedia.org/wiki/Autocorrelaci%C3%B3n.
Debe tenerse en cuenta que:
- Está técnica no es útil con muestras con pocas observaciones.
- Las distancias k entre 1 y 10 son los más informativos.
- En general, distancias k > 20 no aportan información.
| Datos no autocorrelados | Datos autocorrelados |
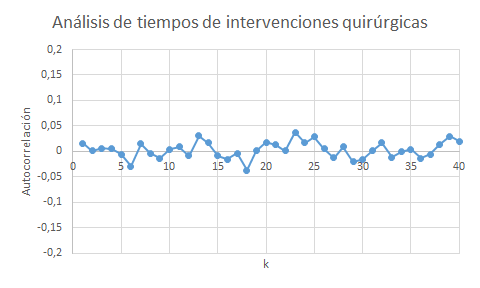 |
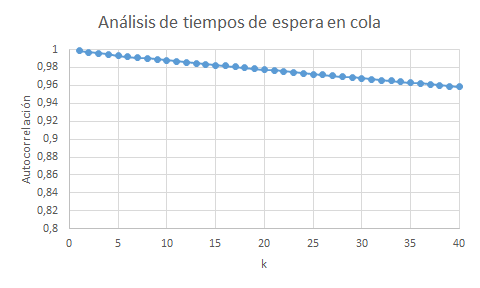 |
Diagramas de dispersión
Se trata de una representación gráfica de la observación k frente a la observación k + 1. Si no hay dependencia entre las observaciones, se debería presentar una nube de puntos sin forma definida. Si la nube de puntos marca claramente una tendencia es que las observaciones no son independientes.
Más información en https://es.wikipedia.org/wiki/Diagrama_de_dispersi%C3%B3n.
Debe tenerse en cuenta que:
- No son útiles con muestras pequeñas (n < 50).
- Si hay una correlación positiva la nube de puntos tendrá forma de recta de pendiente positiva.
- Si hay una correlación negativa la nube de puntos tendrá forma de recta de pendiente negativa.
| Datos dispersos | Datos no dispersos |
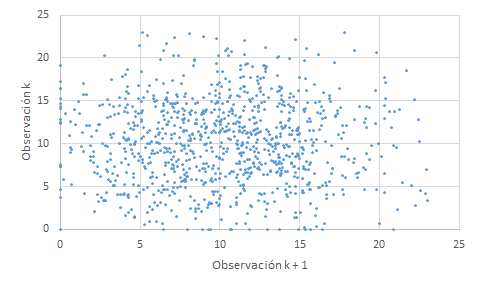 |
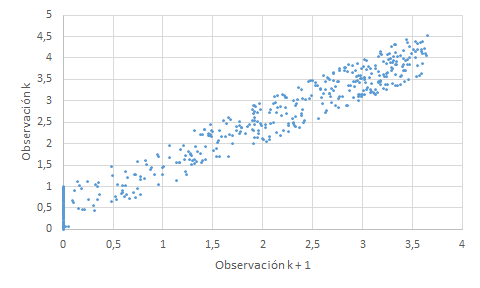 |
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 3.0