Sistemas MIMO

Consideramos en esta sección el caso de sistemas que tienes multiples entradas y salidas (sistemas  MIMO). La representación de estos sistemas puede hacerse a partir de su matriz de transferencia (una matriz cuyos elementos son las funciones de transferencia entre las distintas entradas y salidas) o bien mediante la representación de estados.

Sistemas MIMO a partir de la matriz de transferencia

Para definir estos sistemas se usa igualmente la función tf pero en este caso los argumentos de entrada (numerador y denominador) son celdas que contienen las numeradores y denominadores de cada función de transferencia que constiyuye la matriz de transferencia. De tal modo que para un sistema de mxn (m entradas y n salidas) se debe crear una celda de dimensión mxn con los numeradores de las funciones de transferencia y una celda con la misma dimensión con los denominadores de la funciones de transferencia.

El elemento {i,j} de la celda del numerador  se corresponde con el numerador de la función de transferencia de la entrada j a la salida i. Igualmente para la velda de denominadores, el elemento {i,j} de la celda del denominador se corresponde con el denominador de la función de transferencia de la entrada j a la salida i.

Para ilustrar esto, consideremos el siguiente sistema 2x2:

Y₁(s)=G₁₁(s)U₁(s)+G₁₂(s)U₂(s)
Y₂(s)=G₂₁(s)U₁(s)+G₂₂(s)U₂(s)

Gráficamente el diagrama de bloques de este sistema sería:

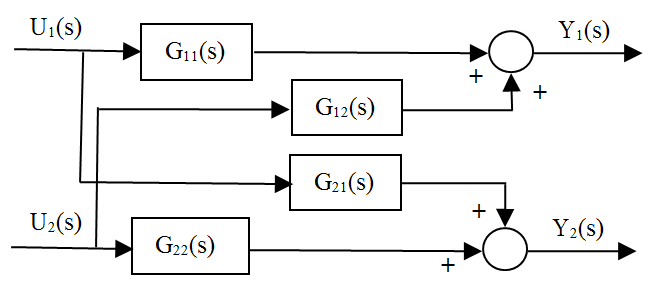
Supongamos que las funciones de transferencia son:

G11(s)=11/(s+1)
G12(s)=12/(s+2)
G21(s)=21/(s+3)
G22(s)=22/(s+4)

La representación de este sistem en Octave se relizaría con el siguiente código:

num{1,1}=11;num{1,2}=12;
num{2,1}=21;num{2,2}=22;
den{1,1}=[1 1];den{1,2}=[1 2];
den{2,1}=[1 3];den{2,2}=[1 4];
sys=tf(num,den);

Obsérvese que se deifne una celda para alamcenar los numeradores y denominadores, y que el elemento i,j de cada celda se corresponde con el numerador/denominador de la función de transferencia desde la entrada j a la salida i.

Sistemas MIMO a partir de la representación de estados

La forma más sencilla de representar un sistema MIMO es mediante la representación de estados. Lo que diferenciará a un sistema SISO de un MIMO son las dimensiones de las matrices B, C, y D. Si la matriz B y D tienen más de una columna, entonces el sistema que representa tiene más de una entrada (sistema MISO, mutiples entradas y una única salida). Si además las matrices C y D tienes más de una fila, el sistema tiene más de una salida (sistema MIMO).

Como ejemplo de sistema MIMO consideremos el siguiente:

Como se observa este es un sistema de dos entradas y dos salidas. La definición en Octave sería así:

A=[1 5;-2 4];
B=[-7 1;0 3];
C=[1 5;2 -1];
D=[0 1;3 0];
sys=ss(A,B,C,D);