Saltar la navegación

Respuesta temporal de sistemas de 2º orden

Respuesta temporal de sistemas de primer orden

Modelo

Un sistema de primer orden tiene como ecuación diferencial (considerando que la derivada de la entrada no interviene en la respuesta del sistema):

ec1

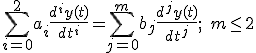
\sum_{i=0}^{2}a_i\frac{d^iy(t)}{dt^i}=\sum_{j=0}^{m}b_j\frac{d^jy(t)}{dt^j};\;m\leq{2}

 Para obtener la función de transferencia, aplicamos la transformada de Laplace a la ecuación sin tener en cuenta las condiciones iniciales y despejamos Y(s)/U(s):

ec2

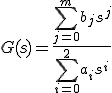
G(s)=\frac{\sum_{j=0}^{m}b_js^j}{\sum_{i=0}^{2}a_is^i}

En esta sección estudiaremos un caso particular de sistemas de segundo orden: el caso en el que en la ecuación diferencial no intervienen derivadas de la función de entrada. Para estos sistemas la función de transferencia se puede expresar del siguiente modo (consideraremos que la ganancia estacionaria es igual a 1): 

ec 3

G(s)=\frac{w_n^2}{s^2+2\delta w_ns+ w_n^2}

donde δ se conoce como factor de amortiguamiento y wn es la frecuencia natural.

Los polos de este sistema se calculan resolviendo s2+2δwns+wn2=0:

s=\frac{-2\delta w_n \pm \sqrt{4\delta^2w_n^2-4w_n^2}}{2}=-\delta w_n\pm \sqrt{\delta^2-1}=-\delta w_n\pm j\sqrt{1-\delta^2}

La respuesta del sistema dependerá de donde estén ubicados estos polos. La ubicación dependerá de los valores que tome δ. Así, hay 4 posibilidades son:

  1. δ=0, raíces imaginarias puras.
  2. 0<δ<1, raíces complejo conjugadas.
  3. δ=1, raíces reales e iguales.
  4. δ>1, raíces reales y distintas.

i)  δ=0. Funcionamiento libre (o sin amortigumiento). La respuesta a un entrada escalón de amplitud 1 es:

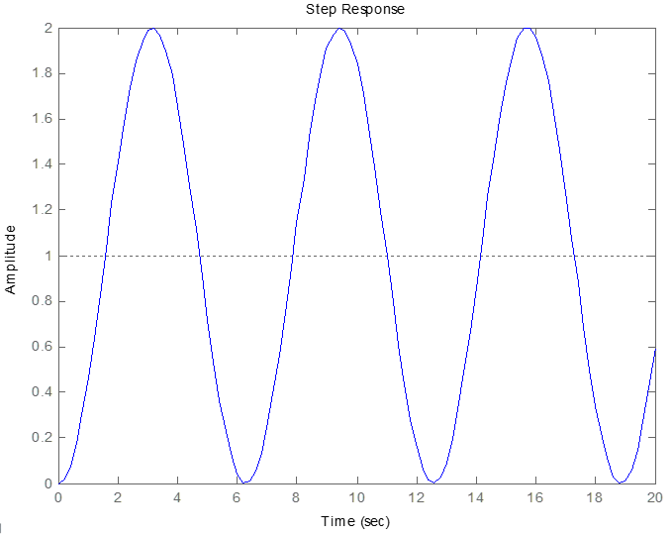
ii)  0<δ<1. Funcionamiento con amortiguamiento subcrítico. La respuesta a un entrada escalón de amplitud 1 es:

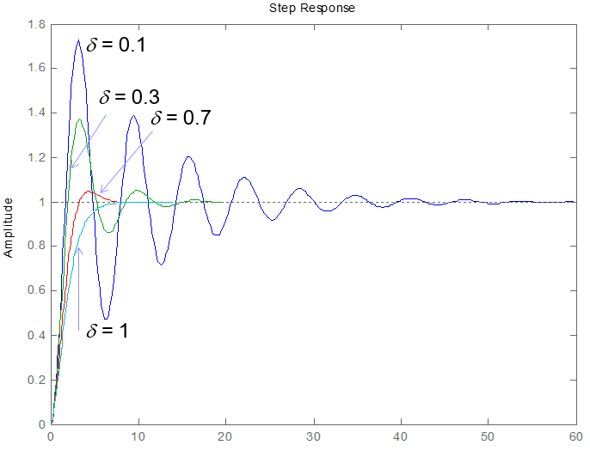
iii)  δ=1. Funcionamiento con amortiguamiento crítico. La respuesta a un entrada escalón de amplitud 1 es:

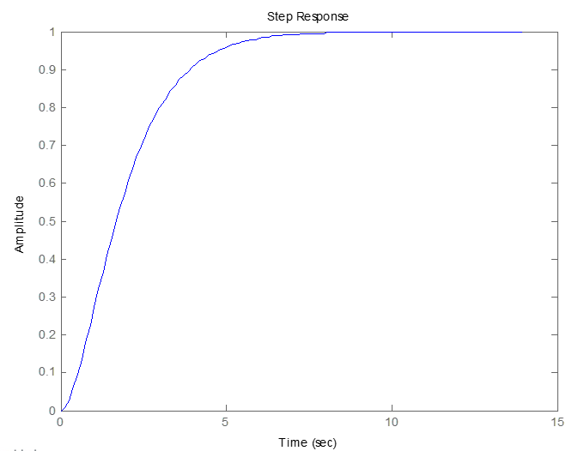
iv)  δ>1. Funcionamiento con amortiguamiento supercrítico. La respuesta a un entrada escalón de amplitud 1 es:

Actividad multimedia: simulación y análisis de la respuesta temporal de sistemas de segundo orden.