Saltar la navegación

Introducción

Introducción

Uno de los aspectos básicos en el análisis de sistemas lineales invariantes en el tiempo (LTI) es estudiar su respuesta temporal.Este estudio se centra conocer cómo responde un sistema cuando se la aplica una entrada determinada.

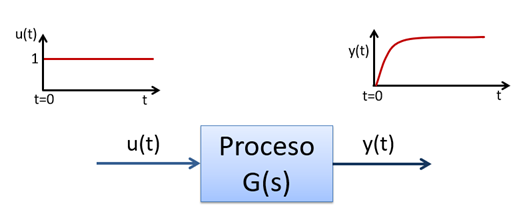
Figura 1. Ejemplo de respuesta temporal de un sistema (y(t) ante una entrada escalón (u(t).

La respuesta temporal se divide en dos partes:

  • Respuesta transitoria: parte de la respuesta temporal que tiende a cero cuando el tiempo tiende a infinito. La define la parte de real de s.
  • Respuesta permanente o estacionaria: parte de la respuesta temporal que permanece una vez que la transitoria ha desaparecido. La define la parte imaginaria de s.

Normalmente las entradas que se consideran para analizar la respuesta temporal son:

  • Entrada impulso:

u(t) = \begin{cases} \infty, & \mbox{si } t=0 \\ 0, & \mbox{si } t \neq 0\end{cases}

Cuya expresión en el dominio transformado es 

U(s)=1

 

  • Entrada escalón unitario:

u(t) = \begin{cases} 0, & \mbox{si } t<0 \\ R, & \mbox{si } t \geq 0\end{cases}

Cuya transformada es

U(s)=R/s

  • Entrada rampa:

u(t) = \begin{cases} 0, & \mbox{si } t<0 \\ Rt, & \mbox{si } t \geq 0\end{cases}

Cuya transformada es

U(s)=R/s^2

En Octave los comandos para la simulación de estas entradas son impulse (para la entrada impulso), step (para la respuesta escalón)  y  la simulación de entradas en rampa puede hacerse con la función lsim.

En esta sección nos centraremos en el estudio de la respuesta temporal de sistemas de primer y segundo orden ante una entrada escalón unitario.