Saltar la navegación

Respuesta temporal de sistemas de 1er orden

Respuesta temporal de sistemas de primer orden

Modelo

Un sistema de primer orden tiene como ecuación diferencial (considerando que la derivada de la entrada no interviene en la respuesta del sistema):

ec1

\frac{dy(t)}{dt}+ay(t)=Ku(t)

 Para obtener la función de transferencia, aplicamos la transformada de Laplace a la ecuación sin tener en cuenta las condiciones iniciales:

ec2

sY(s)+aY(s)=KU(s)

Entonces la función de transferencia del sistema es:

ec 3

G(s)=\frac{Y(s)}{U(s)}=\frac{K}{s+a}

Si definimos los parámetros:

ec4

K_{dc}=\frac{K}{a}; \; \tau=\frac{1}{a}

La función de transferencia también se podría expresar como:

ec 5

G(s)=\frac{K{dc}}{\tau s+1}

La ecuación característica del sistema es s+a=0. Como vemos, solo existe un polo que está ubicado en s=-a.

Respuesta temporal

Para obtener la respuesta temporal del sistema ante una entrada u(t)=R, despejamos Y(s) de la función de transferencia:

ec 6

Y(s)=\frac{K}{s+a}U(s)

Teniendo en cuenta que U(s)=R/s, la salida quedaria:

ec 7

Y(s)=\frac{KR}{s(s+a)}

Entonces y(t) se puede obtener antitransformando Y(s). Para ello, descomponemos en fracciones simples y una vez que tenemos Y(s) descompuesto en fracciones simples, podemos obtener la antitransformada mirando en las tablas de transformadas de Laplace.

Descomponemos Y(s):

ec 8

Y(s)=KR(\frac{A}{s}+\frac{B}{s+a})

Las constantes A y B se pueden obtener así:

ec 10

A=s\frac{1}{s(s+a)}|_{s=0}=\frac{1}{a}

ec 11

A=(s+a)\frac{1}{s(s+a)}|_{s=-a}=-\frac{1}{a}

Por lo tanto, y(t) resulta ser:

ec 12

y(t)=L^{-1}(Y(s))=\frac{KR}{a}(1-e^{-at})

o de otra forma:

ec 14

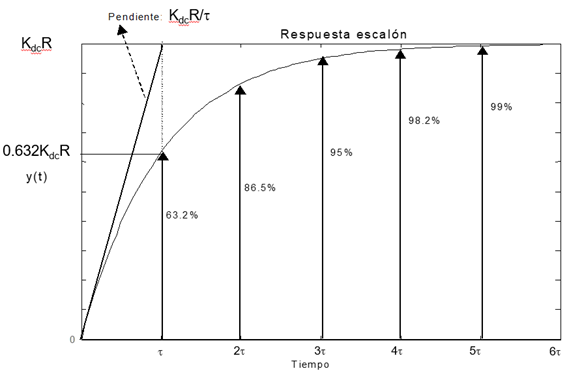
y(t)=K_{dc}R(1-e^{-t/\tau})

La representación de esta respuesta es la que se muestra en la siguiente figura:

fig 1

Sistemas de primer orden con retardo

Cuando el proceso viene afectado por un retardo, entonces es necesario incorporar este elemento al modelo anterior. Un elemento de retardo se modelo mediante el término exponencial:

,

donde tm representa el tiempo de retardo (en la unidad correpondiente: segundos, minutos, ...). Por lo tanto, un sistema de primer orden con retardo quedaría descrito por la función de transferencia:

La respuesta escalón de este tipo de procesos sería como la representada enteriormente, pero desplazada en el tiempo un intervalo igual a tm.

Ejemplo: La respuesta antes una entrada escalón unitario del proceso :

sería la que se muestra en la figura siguiente:

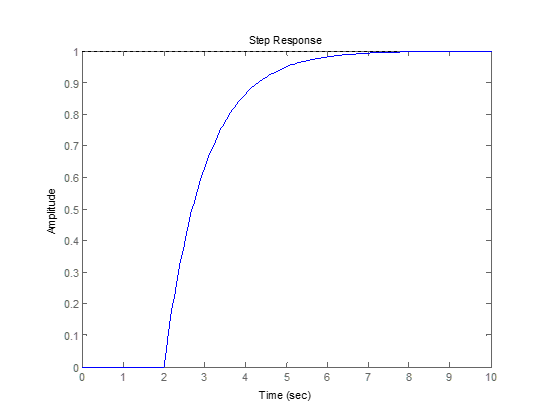
Se debe observar que en este caso el tiempo muerto es 2, la constante de tiempo es 1 y la ganancia también es 1. Como se aprecia, en este caso el tiempo en que la salida alcanza el 63% del valor estacionario (t63) no coincide con la constante de tiempo (τ). La relación ahora es: τ=t63-tm.

Actividad multimedia:  Análisis y simulación de sistemas de primer orden.

Modelado empírico de sistemas de primer orden

Como es sabido hay dos estrategias fundamentales para el modelado de procesos industriales:

  • Modelado teórico: se deducen las ecuaciones que rigen la dinámica del proceso a partir de los principios físico-químicos que lo gibiernan.
  • Modelado empírico: el modelo se obtiene a partir de la experimentación. Se propone un experimento sobre el proceso real y se trata de ajustar la respuesta observada a un modelo.

La mayoría de los procesos en la industria son de primer o segundo orden. Es muy habitual que la respuesta escalón de muchos procesos industriales sea como la siguiente:

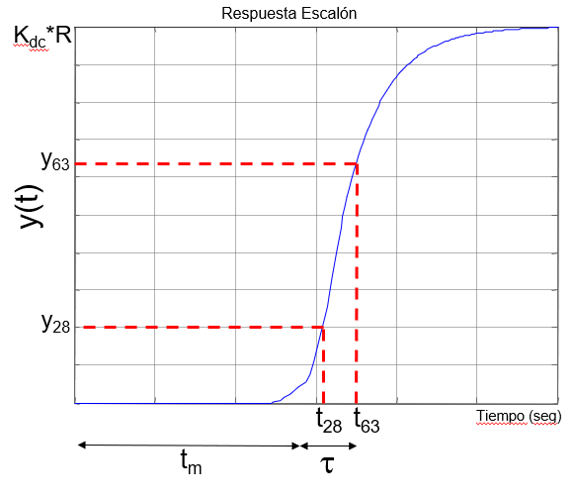
Este tipo de respuesta en forma de "S" puede aproximarse por un modelo de primer orden con un retardo. Para obtener los parámetros de la función de transferencia (Kdc,  τ y tm) se procede del siguiente modo:

  • Obtención de la ganancia estática, Kdc: asumiendo que la entrada escalón aplicada es de magnitud R y que ys es el valor estacionario que alcanza la salida. La ganancia estática puede obtenerse como:

  • Obtención de la constante de tiempo, τ: para obtener la constante de tiempo (que debe obtenerse previamente a la obtención dle tiempo muerto, tm) se debe calcular los valores de la salida en el 63% del valor final (y63) y en el 28% del valor final(y28). Para cada uno de estos valores, calcularemos el  constante de tiempo correspondiente (t63 y t28). a partir de aquí, la constante de tiempo del sistema se puede aproximar por:

Obtención del tiempo muerto, tm: el tiempo muerto se puede aproximar por 

Hay que tener en cuanta que esto no es más que un modelo aproximado para describir el comportamiento real observado. Por otra parte, existen otras alternativas para obtener estos parámetros, pero esta es una de las opciones más sencillas que ofrece buenos resultados.

Actividad multimedia: modelado empírico