Digital signals and sampled systems
Discrete-time systems
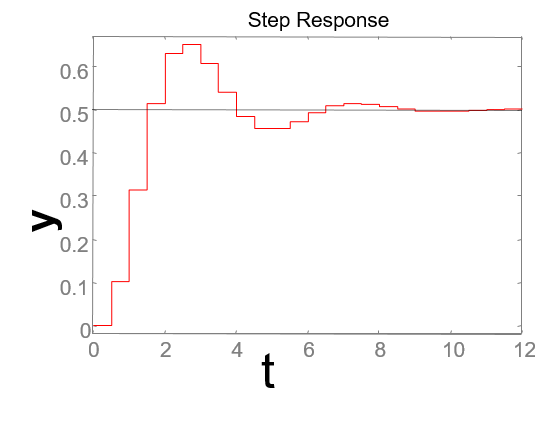
In discrete-time systems variables are sampled and quantized (we will not consider sample-data signals that can take any value into a range). Then, variables will change every T seconds. T is called sample time. A typical response of a discrete time system will look like in the figure:
The sample and hold process of a continuous signal is represented in the following figure:
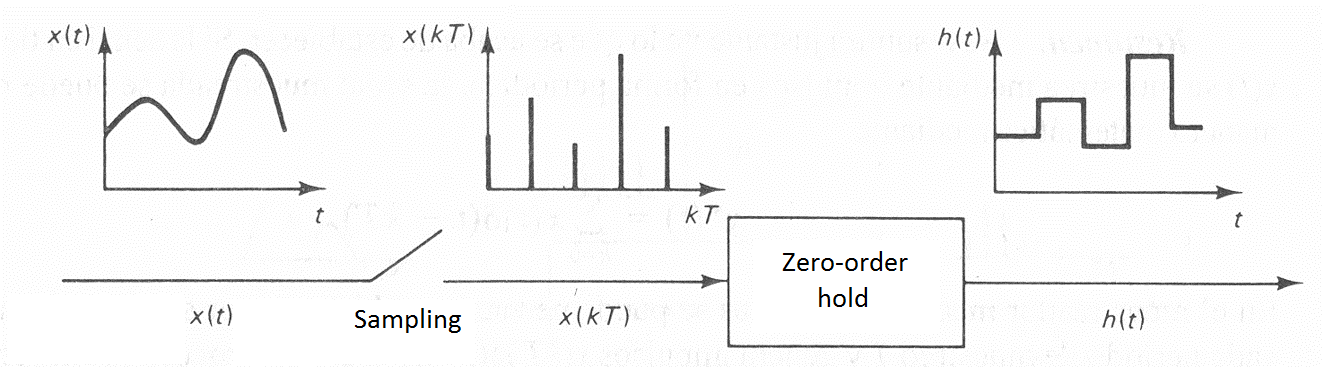
If we consider the values of the resulting signal of the sampling process of x(t), x(kT):
x(0*T), x(1*T), x(2*T),...
Relation between s and z plane
All continuous functions that have Laplace Transform, also have Z transform. The relation between both planes is given by teh expression ![]() :
:
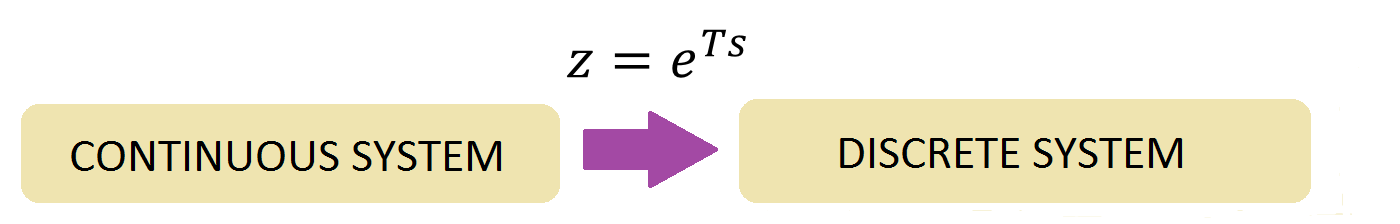
Inverse transform
The inverse transform of a variable can be done from the definition of the Z-transform. However, if the signal is a polynomial fraction, that is common in control engineering, the inverse transform can be obtained using fraction decomposition and then uusing the Z transform tables for the resulting single terms.
Properties of the Z-transfer function
Some of the properties of the Z-trasform are presented. These have special relevance from the modelling and control design perspective.
Linearity
![]()
Multiplying by a constant Multiplicación por una constante:
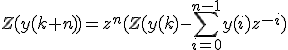
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 3.0