Gráficos p y c

Los gráficos p y c son los gráficos de control usados para datos de tipo discreto, es decir, el número total de defectos por unidad producida o el número total de unidades defectuosas.

Gráficos p

Los gráficos p se usan para datos de tipo sí/no. Pueden mostrar, por ejemplo, el total de unidades defectuosas dividido por el total de unidades producidas. Este tipo de gráficos se basa en la distribución de probabilidad binomial, y son válidos en tanto la probabilidad p de que una unidad "falle" es la misma para todas las unidades producidas.

Los límites de control de este tipo de gráficos se definen como sigue:

Límite de control superior (UCL)	Línea central	Límite de control inferior (LCL)

Donde:

p es la proporción media de unidades defectuosas en cada muestra;

 es la desviación estándar de la distribución de las muestras, con n = tamaño de cada muestra;

y los valores típicos para z son 2 (más restrictivo) o 3 (menos restrictivo).

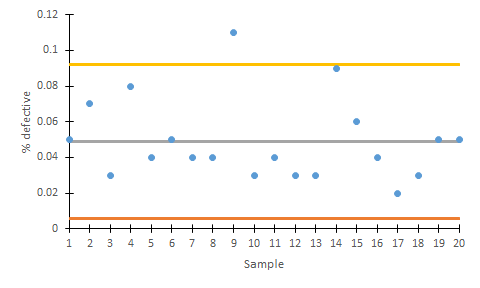
Construyendo gráficos p

1. Tomar 20-25 muestras de, al menos, unas 100 piezas/productos cada una. Calcular la proporción de piezas defectuosas en cada muestra p.
2. Calcular la proporción media de piezas defectuosas (p).
3. Fijar los límites deseados (generalmente 3σ) y calcular los límites de control
4. Dibujar las muestras en los gráficos.
5. Analizar los resultados y tratar de identificar las posibles causas imputables de variación

Gráficos c

Los gráficos c muestran el número de defectos por unidad. Este tipo de gráficos se basa en la distribución de probabilidad de Poisson. 

Los límites de control de este tipo de gráficos se definen como sigue:

Límite de control superior (UCL)	Línea central	Límite de control inferior (LCL)

Donde:

c es la media de defectos por unidad;

y los valores típicos para z son 2 (más restrictivo) o 3 (menos restrictivo).

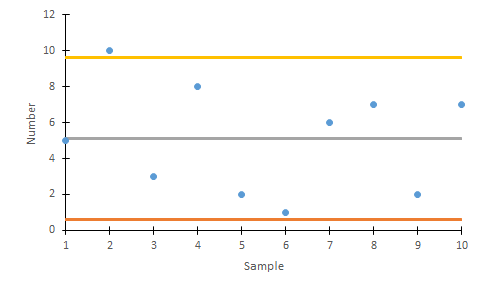
Construyendo gráficos c

1. Tomar 20-25 muestras de 1 pieza/producto cada una. Contar el número de defectos de cada unidad c.
2. Calcular el número medio de defectos por unidad (c).
3. Fijar los límites deseados (generalmente 3σ) y calcular los límites de control
4. Dibujar las muestras en los gráficos.
5. Analizar los resultados y tratar de identificar las posibles causas imputables de variación