Evolución Dinámica (Matemáticamente)
En el caso de plantear la evolución Dinámica desde el punto de vista matemático es necesario representar la Red de Petri de forma matricial, esto es:
- Matriz de incidencia previa:
C- = [cij-] donde cij- =a (pi,tj) .
Dicha matriz define las conexiones de las transiciones con los lugares previos.
- Matriz de incidencia posterior:
C+=[cij+] donde cij+=b(pi,tj).
Dicha matriz define las conexiones de las transiciones con los lugares posteriores.
Basándose en las dos Matrices planteadas anteriormente se define la Matriz de Incidencia como:
C=C+-C-
Ejemplo:
Podemos determinar la Matriz de Incidencia de la siguiente Red de Petri.
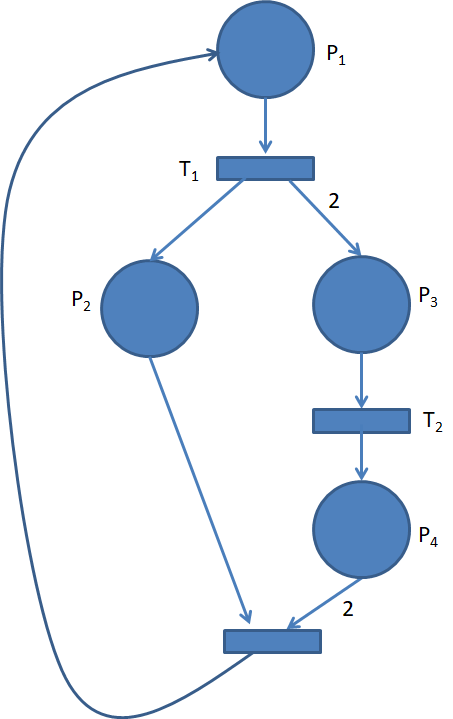
La Matriz de Incidencia será:
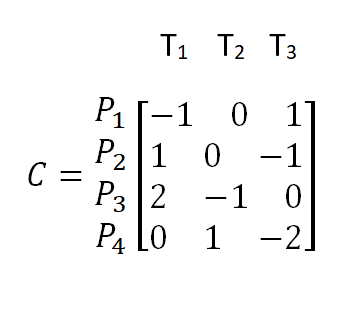En este caso la Evolución Dinámica esta definido por la variación del marcado M(k), esto es:
donde σ(k) corresponde al vector de disparo, cuya dimensión coincide con el número de transiciones y, además, el elemento σj(k) es 1 ó 0 si la transición Tj se ha disparado o no, respectivamente.
Relación entre la representación Gráfica y Matemática.
Basándose en lo anterior se puede relacionar la evolución Dinámica de ambas representaciones, gráfica y matemática .
Determinar la evolución de marcado de la siguiente Red de Petri con un marcado inicial dado gráficamente.
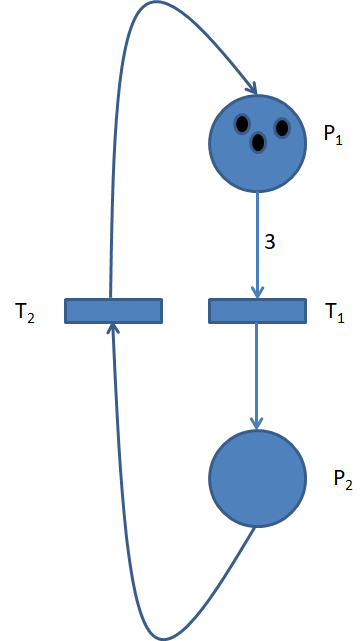
En general, la ecuación dinámica se puede expresar de la siguiente manera:
, donde
.
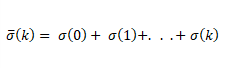