Definición de Redes de Petri

Las Redes de Petri  permiten modelar cualquier sistema de eventos discretos. Dicha modelización puede ser descrita  gráficamente o matemáticamente.

Descripción Gráfica.

La Representación Gráfica tienen tres elementos básicos, que son: lugares (P), Transiciones (T) y Arcos. Dentro de estos últimos podemos distinguir entre arcos Previos (Arco de unión entre lugar y transición) y Posteriores (Arco de unión entre transición y lugar). 

Al igual que la representación Matemática es necesario incluir la evolución temporal o dinámica, para ello utilizaremos el Marcado, se representan mediante puntos en los lugares.

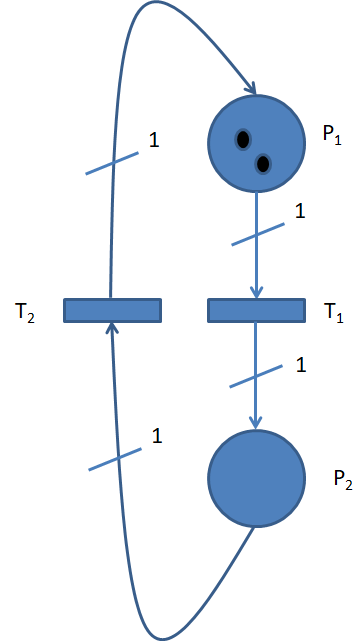
Ejemplo de Representación Gráfica de Red de Petri.

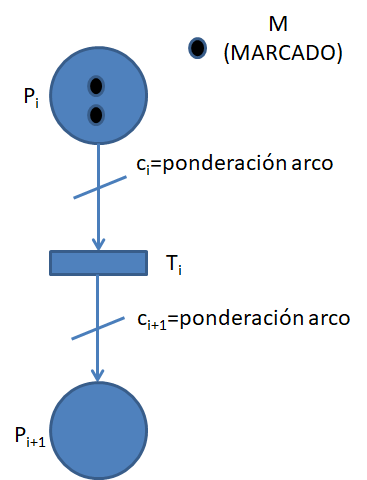
Descripción Matemática.

 La representación matemática se define como un conjunto R={P,T,a,b} donde:

- P es el conjunto de Lugares.

-T es el conjunto de Transiciones.

- a es aplicación de incidencia previa. a: P x T -> N (número naturales) con a(pi,tj) =ponderación del arco de unión del lugar pi con la transición tj.

    Esta aplicación nos indica como están conectadas las transiciones con los lugares previos a las transiciones.

- b es la aplicación de incidencia posteriore. b: P x T -> N (número naturales) con b(pi,tj) =ponderación del arco de unión de la transición tj con el lugar pi

   Esta aplicación nos indica como están conectadas las transiciones con los lugares posteriores a las transiciones.

Por último el marcado  M en esta representación se considera como una aplicación  M: P-> N , básicamente indica el número de marcas asociadas a cada lugar. 

Basándonos en lo anterior la Red de Petri Marcada se define como el conjunto {R,M}.