Manejo de polinomios
Representación
En Octave no hay un tipo de datos especial para representar a los polinomios. Lo que ocurre es que todas las funciones para el manejo de polinomios usan un mismo convenio para su representación. Se utiliza un vector fila que contiene los coeficientes en orden descendente.
Dado el vector p=[c1,c2,...,cN], éste representa al polinomio
![]()
Como se ve, un polinomio de orden N-1 se representa por un vector de N elementos.
Si en el polinomio original falta el sumando de algún orden, en el vector que representa a dicha polinomio no se puede suprimir el elemento correspondiente, sino que hay que hacer su valor igual a 0. Si suprimiéramos un elemento, el Octave entendería que el polinomio es de orden N-2.
Para confirmar cómo entiende el Octave el polinomio que tenemos definido, es conveniente utilizar la función polyout:
- polyout(p,x)
- muestra por pantalla una representación del polinomio p, usando como carácter para la variable independiente el indicado en string x, que por defecto vale "s".
Ejemplos |
|
|
|
Funciones
Operación con polinomios
Las funciones que realizan operaciones con polinomios son:
- polyreduce(p)
- reduce, si es posible, el tamaño del vector del polinomio p, quitando los ceros a la izquierda.
- conv(p,q)
- devuelve el producto de dos polinomios.
- [c,r]=deconv(x,y)
- devuelve el cociente y el resto de la división del polinomio x entre el y.
- [r,p,k,e]=residue(num,den)
- calcula la descomposición en fracciones simples del cociente del polinomio num entre el den. r son los residuos (numeradores), p son los polos (denominadores), k es el cociente (si grado del numerador es mayor que el del denominador), y e son los exponentes para cada denominador. Es decir:
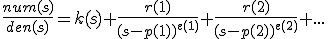
- polyderiv(p)
- devuelve el polinomio derivada de p.
La suma (resta) de polinomios consiste, sencillamente, en sumar sus coeficientes. Si lo polinomios están representados por vectores de la misma longitud, se podrás utilizar directamente la suma de matrices:
psuma = p1 + p2
pero si no tienen la misma longitud, hay que rellenar el más corto con ceros por la izquierda antes de sumar los vectores. Un código que haría esto de manera general es el siguiente:
l1 = length(p1); l2=length(p2);
psuma = polyreduce( [ zeros(1, l2-l1), p1] + [zeros(1, l1-l2), p2] )
donde se ha aprovechado que la función zeros devuelve la matriz vacía si algunos de sus parámetros (dimensión solicitada) es negativo. Se a aplicado polyreduce por si, al operar, se hace cero el coeficiente de mayor grado.
Ejemplos |
|
dados los polinomios
|
|
Cálculo de polinomios
Las funciones que realizan cálculos con polinomios son:
- polyval(p,X)
- evalúa el polinomio p para todos los elementos de X y devuelve una matriz de la mima dimension que X.
- polyvalm(p,A)
- para A matriz cuadrada, evalúa el polinomio p en sentido matricial.
- roots(p)
- devuelve un vector columna con las raíces del polinomio.
- poly(r)
- siendo r un vector, devuelve el polinomio cuyas raíces son los elementos de r.
- poly(A)
- siendo A matriz cuadrada, devuelve el polinomio característico.
- polyfit(x,y,n)
- devuelve el polinomio de orden n que mejor se ajusta, en mínimos cuadrados, a los puntos formados por los pares ordenados (x,y) formados por los valores en x e y.
Ejemplos |
|
|
|
Obra colocada bajo licencia Creative Commons Attribution Non-commercial Share Alike 3.0 License