Operandos y funciones generales en Octave
Funciones Matemáticas
Matriciales
Son funciones que están definidas matemáticamente para una matriz como un todo.
Trascendentes
- expm(A)
- Exponencial de una matriz cuadrada, se calcula por desarrollo de la serie de Taylor.
- logm(A)
- Logaritmo neperiano de una matriz cuadrada.
- sqrtm(A)
- Raíz cuadrada de una matriz cuadrada.
Generales
- det(A)
- determinante de una matriz cuadrada.
- trace(A)
- traza de la matriz: suma de los elementos de su diagonal principal.
- inv(A)
- inversa de una matriz. A debe ser cuadrada no singular ( det(A)!=0 ).
- inverse(A)
- equivalente a inv(A)
- landa=eig(A)
- autovalores de la matriz cuadrada.
- [v,landa]=eig(A)
- devuelve los autovectores y autovalores de la matriz cuadrada.
- rank(A)
- rango de la matriz.
Ejemplos |
|
|
|
Elemento-a-elemento
Funciones que se aplican a cada elemento de la matriz y el resultado se devuelve en una matriz de las mismas dimensiones. Están definidas todas las habituales en cualquier lenguaje de programación o librería matemática.
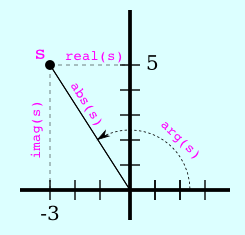
Aritmética compleja
- abs(X)
- módulo del número complejo, si son reales es equivalente al valor absoluto.
- arg(X) angle(X)
- argumento del número complejo.
- conj(X)
- complejo conjugado, devuelve el mismo número pero con la parte imaginaria cambiada de signo.
- imag(X)
- devuelve solo la parte imaginaria de los elementos y como número real.
- real(X)
- devuelve sólo parte real de los elementos.
Utilitarias
- ceil(X) floor(X) fix(X) round(X)
- redondeos hacia menos infinito, hacia más infinito, hacia cero y hacia el entero más cercano.
- rem(X,Y)
- resto de la división de X entre Y.
- sign(X)
- signo de los elementos: 1 si positivo, -1 si negativo, 0 si igual a 0.
Trascendentes
- exp(X) log(X) log10(X) log2(X)
- exponencial, logaritmo neperiano, logaritmo decimal y logaritmo de base 2.
- pow2(X)
- para cada elemento se calcula 2x, es equivalente a 2.^X
- sqrt(X)
- raíz cuadrada.
- sin(X) cos(X) tan(X) sec(X) csc(X) cot(X)
- trigonométricas ordinarias: seno, coseno, tangente, secante, cosecante y contangente
- asin(X) acos(X) atan(X) asec(X) acsc(X) acot(X)
- trigonométricas inversas: arcoseno, arcocoseno, arcotangente, arcosecante, arcocosecante y arcocotangente.
- sinh(X) cosh(X) tanh(X) sech(X) csch(X) coth(X)
- trigonométricas hiperbólicas: seno hiperbólico, coseno hiperbólico, tangente hiperbólica, secante hiperbólica, cosecante hiperbólica y contangente hiperbólica.
- asinh(X) acosh(X) atanh(X) asech(X) acsch(X) acoth(X)
- trigonométricas hiperbólicas inversas: arcoseno hiperbólico, arcocoseno hiperbólico, arcotangente hiperbólica, arcosecante hiperbólica, arcocosecante hiperbólica y arcocotangente hiperbólica.
- atan2(y,x)
- arcotangente de y/x pero con el argumento correcto entre -π y +π.
Ejemplos |
|
|
|
Obra colocada bajo licencia Creative Commons Attribution Non-commercial Share Alike 3.0 License