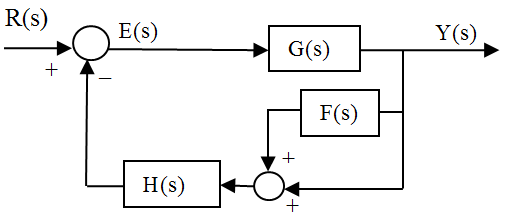
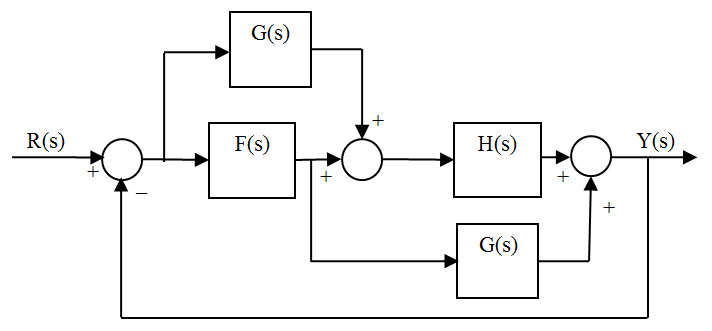
Reducción de diagramas de bloques
La función que usaremos para reducir diagramas de bloques connect. La sintaxis de esta función es la que se indica a continuación:
syslc=connect(sys,cm,inputs,outputs)
donde
- sys es un sistema que "contiene" a todos los sistemas que intervienen en el diagrama y se genera con la función append.
- cm es una matriz de conexiones. Esta matriz indicaría cómo están conectados los sistemas entre sí. Para poder hacer esto se debe numerar cada bloque que intervenga en el sistema. También habría que asignar un número a cada entrada y a cada salida de cada bloque, empezando por la primera entrada del bloque 1 y avanzando siguiendo el orden en que se hayan numerado los bloques del diagrama. Si todos los bloques sólo tienen una entrada y una salida, entonces el numero de entrada y el de salida siempre coinciden con el número de bloque.
- inputs define las entradas externas del sistema. Es un vector que indica a que número de entrada se suma la entrada externa. Si sólo hubiera una entrada al sistema, la variable inputs sería un escalar, de lo contrario inputs tendría tantos valores como entradas.
- outputs define las salidas del sistema. Es un vector que contiene los números de salida que van a tomarse como salida del sistema global.
Ejemplo:
Para ilustrar el funcionamiento de connect, consideremos el sistema que se muestra en la figura:
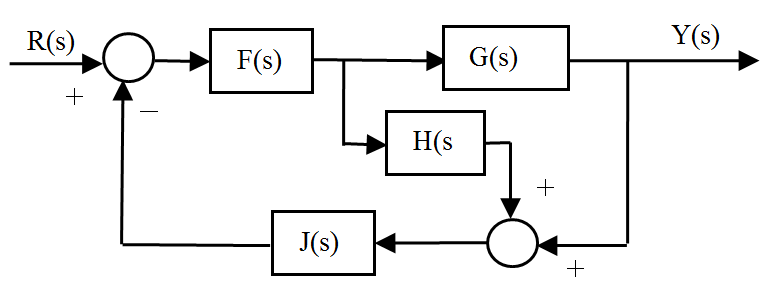
donde
![]() ,
, ![]() ,
, ![]() ,
, ![]()
El procediminiento para reducir el diagrama mediante la función connect es el siguiente:
1.- Definir los sistemas en Octave con las funciones tf, zpk o ss:
sysf=tf(10,[1 9]);
sysf=tf([1 2],[1 9 18]);
sysh=tf(5,1);
sysj=zpk(-4,[-2 -5],3);
2.- Numerar los bloques que intervienen en el diagrama de bloques. En nuestro caso consideraremos la numeración de la figura (se puede tomar cualquier otra):
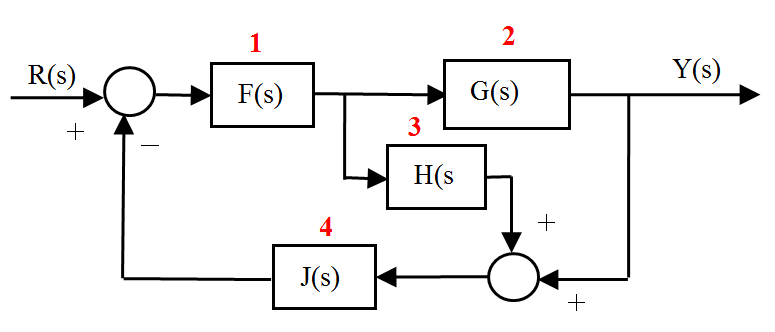
3.- Numerar cada entrada y cada salida del diagrama empezando siguiendo el orden definido en el paso anterior.
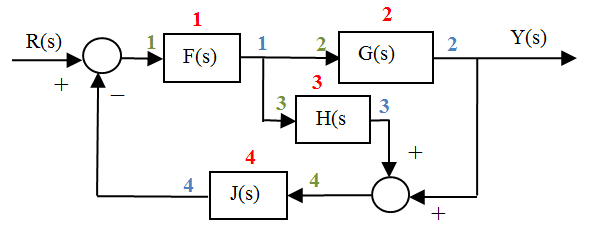
Evidentemente si todos los sistemas son SISO (una entrada y una salida) el número de entrada y de salida coincide con el del bloque. Si no fuese así, entonces hay que tenerlo en cuenta, de tal modo que si el bloque 1 tuviera 2 salidas, la salida del bloque 2 sería la número 3, etc.
Si todos los sistemas que integran el diagrama son SISO este paso 3 puede evitarse ya que el número de cada entrada o salida coincide con el del bloque.
4.- Agrupar todos los sistemas en un único sistema con la función append:
syst=append(sysf,sysg,sysh,sysj);
Hay que tener en cuenta que el orden en que se ponen los sistemas en la función append debe coincidir con el orden que hayamos elegido en el paso 2.
5.- Definir la matriz de conexiones. Debemos crear una matriz donde le indicamos al motor de Octave cómo están conectados los bloques del diagrama. La primera columna de esta matriz hace referencias a las entradas de cada bloque. En nuestro ejemplo tenemos 4 bloques con una única entrada cada uno de modo que sólo tendremos cuatro entradas (de la 1 a la 4). Por tanto, la primera columna de la matriz será:
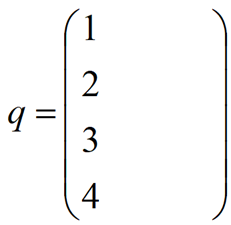
Después se va rellenando cada fila de la matriz indicando las salidas a partir de las cuáles se genera la entrada de esa fila. Por ejemplo, la entrada 1 se genera a partir de la salida 4. Aunque en este caso hay que tener en cuenta el signo del sumador por el que pasa la señal. En esta etapa no se consideran las entradas externas que entran al diagrama (R(s)). Por lo tanto, en esa fila hay que completar con un -4:
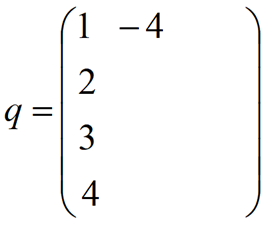
De forma similar se va completando la matriz de conexiones: la entrada 2 se genera a partir de la salida 1, la entrada 3 también se genera a partir de la salida 1 y la entrada 4 se genera a partir de la salida 2 y la 3. Por tanto la matriz q quedaría así:
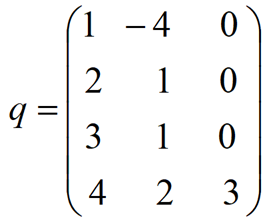
Obsérvese que los huecos que quedan en la matriz se completan con ceros para poder definirla en Octave.
6.- Definir las entradas. Se refiere a las entradas externas a nuestro sistema (R(s)). Tenemos que indicar a qué número de entrada se suma esta entrada externa. En nuestro caso R(s) se está sumando a la entrada del bloque 1, que también es la entrada 1. Por tanto:
inputs=1;
7.- Definir las salidas. Hay que indicar qué número de salida de bloque es la salida del sistema (Y(s)). En nuestro caso Y(s) coincide con la salida del bloque 2, y su número asociado es el 2 también (debido a que al ser sistemas SISO el número de entradas y salidas coincide con el del bloque).
outputs=2;
8.- Llamar a la función connect para definir el sistema Y(s)/R(s).
syslc=connect(syst,q,inputs,outputs)
Esta función devuelve en syslc la representación del sistema en lazo cerrado. Ahora ya se podría analizar el sistema. simular, etc.
Ejemplo: Reducción de un diagrama de bloques con connect |
|
|
Considérese el problema de la figura donde: Definir el sistema Y(s)/R(s) usando el comando connect. |
|
Uso de bloques adicionales para reducir diagramas con connect
Bloque auxiliar a la entrada
En ocasiones es necesario el uso de bloques adicionales con función de transferencia unidad para reducir el diagrama de bloques. A modo de ejemplo considérese la siguiente figura:
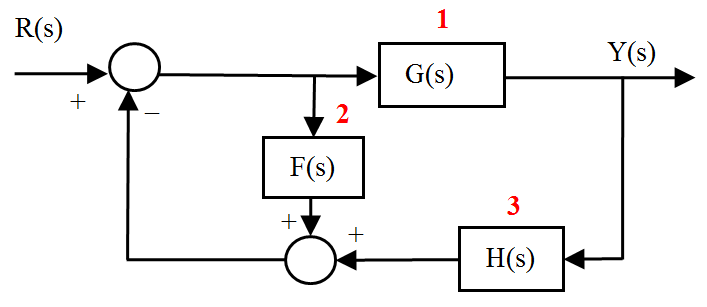
Este es un sistema con una entrada (R(s)) y una salida (Y(s)). El problema que surge es que en la definición de las entradas, tal como está el diagrama tendriamos que hacerlo del siguiente modo:
inputs=[1, 2];
Esto es asi ya que R(s) está entrando a los dos bloques. Pero con esta definición lo que resultaría al llamar a la función connect es un sistema con dos entradas (tantas como hemos definido el vector inputs), lo cual no es admisible ya que el sistema sólo tiene una entrada.
La forma de resolver esto es añadiendo un bloque de ganancia unidad (que por lo tanto no afectaría al diagrama de bloques) ubicado tras el signo de suma. En la figura se ilustra cómo quedaría el diagrama modificado:
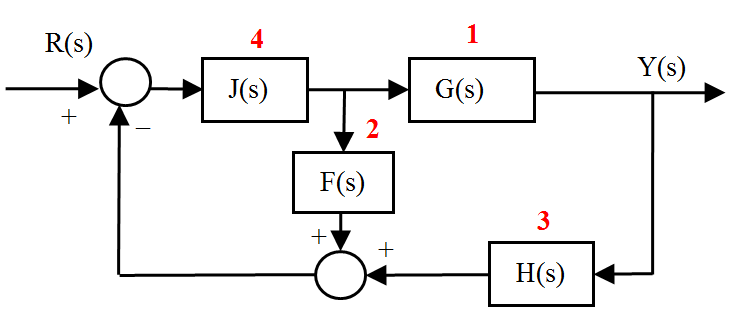
donde J(s) estaría definido así:
sysj=tf(1,1);
La introducción de este bloque adicional hace que haya que redefinir la matriz de conexiones y volver a generar el sistema que contiene a todos los bloques incluyendo este nuevo bloque.
Bloque auxiliar a la salida
Otro caso en el que habría que añadir un bloque es cuando la salida aparece como la suma de dos o más salidas de bloques. Como ejemplo considérese el siguiente diagrama de bloques:
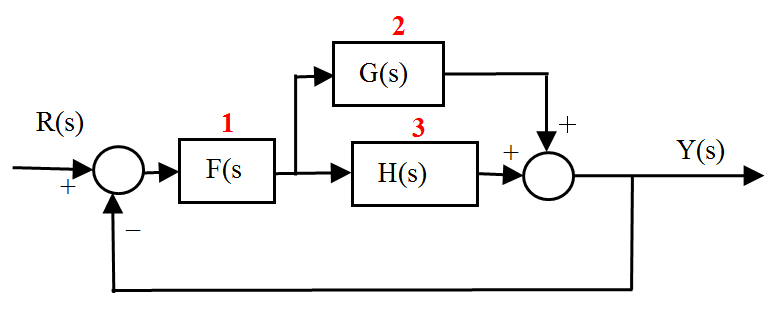
En este caso a la hora de definir la salida habría un problema pues no sabriamos cómo indicar que la salida del sistema es la suma de estas salidas (salidas 2 y 3). Para ello lo mejor es introducir un bloque adicional con función de transferencia unidad cuya única función es que la salida Y(s) sólo tenga una componente. En la figura siguiente se muestra el resultado:
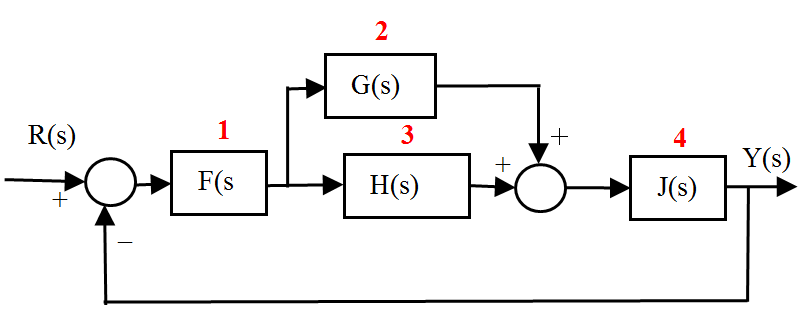
donde J(s) está definido como
sysj=tf(1,1);
Igual que para el caso del bloque auxiliar en la entrada, la inclusión de este bloque auxiliar hace que haya que redefinir la matriz de conexiones y volver a generar el sistema que contiene a todos los bloques incluyendo este nuevo bloque.
Ejemplo: Reducción de un diagrama de bloques con connect usando bloques auxiliares |
|
|
Considérese el problema de la figura de una entrada y una salida, donde:
Definir el sistema Y(s)/R(s) usando el comando connect. |
|